5.6.3 Einzelthemen
Beleuchtungskörper
Verschnitt-Minimierung

Einzelthemen

Verschnitt-Minimierung

Wir haben gesehen dass es nur eine Möglichkeit gibt Pyramiden für Dreiecke zu bilden, und dass diese Kronen sich nicht zur Verschnitt-Minimierung eignen. Einzige Möglichkeit dies zu umgehen ist, wenn wir auf die Ikosaeder-Dreiecksgrenzen verzichten.

Betrachten wir dazu zwei benachbarte Dreiecke des Ikosaeders. Hier sind die Dreiecke pro Ikosaeder-Dreieck gleich gefärbt.

2 Dreiecke mit Pyramide

Es ist nicht gesagt, dass wir unbedingt die Dreiecksfigur beibehalten müssen. So können wir beispielsweise jeweils ein benachbartes kleines Dreieck mitbenutzen. Damit haben wir z. B. zwei Parallelogramme.

2 Parallelogramme mit Pyramide

Und tatsächlich lassen sich mit zwei Parallelogrammen die gleichen Ergebnisse erzielen, wie mit zwei Dreiecken. Wir brauchen wieder drei gleichseitige Dreiecke zur Bildung der Pyramide, aber anstatt an jeder Grundflächen-Kante ein kleines Dreieck anzufügen, fügen wir jetzt nur an einer Grundflächen-Kante ein Dreieck an, eine Grundflächen-Kannte bleibt frei und an der dritten Grundflächen-Kante schließen wir eine Raute bestehend aus zwei kleinen Dreiecken an.

Netz mit Pyramide

Parallelogramm mit Pyramide

Damit entsteht eine Figur, die etwa einer Sphinx ähnelt. Eine Sphinx lässt sich dabei viel besser parkettieren als eine Krone. Noch mehr Möglichkeiten hat man, wenn man noch mehr Ikosaeder-Dreiecke benutzt. Hier lassen sich noch ganz andere Figuren benutzen. Prinzipiell kann man alle 20 Dreiecke dazu hernehmen. Aber dann wird es schnell unübersichtlich. Ich habe die Verwendung von vier Dreiecken in einer Reihe untersucht.

Die Figuren, die aus 6 gleichseitigen Dreiecken bestehen haben in der Mathematik ebenfalls einen eigenen Namen. Sie heißen Hexiamonds. Es gibt insgesamt 12 verschiedene Hexiamonds.

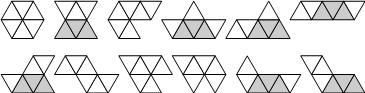
12 Hexiamonds

Allerdings können wir diese nicht alle benutzen. So ist etwa ein regelmäßiges Sechseck, das aus sechs gleichseitigen Dreiecken besteht für uns nicht verwendbar, da sich damit keine Pyramide bilden lässt. Andererseits werden bei den verschiedenen Hexiamonds spiegelverkehrte Figuren miteinander identifiziert. Da wir Papier nur von einer Seite bedrucken, müssen wir solche spiegelverkehrten Figuren jeweils separat führen.

Insgesamt müssen wir uns mit 10 solcher abgewandelter Hexiamonds befassen.

10 abgewandelte Hexiamonds

Wir hätten noch mehr abgewandelte Hexiamonds, wenn wir alle 20 Ikosaeder-Dreiecke betrachten würden. Aber wir können bereits mit vier solcher Hexiamonds unser Problem lösen. Wir können damit für die großen Sterne vier Hexiamonds auf eine DIN A4 Seite mit Klebe- und Wartungskanten drucken. Somit kommen wir bei den großen Sternen weiterhin mit fünf DIN A4 Seiten aus.

wird ergänzt