spaceSticky2
6.1.1.2 Mathematische Hintergründe
Geodätische Kuppeln
Geodätische Kuppeln Beispiele (1,1)
Im Fall Klasse II und (m,n) = (1,1) haben wir drei kleine graue Dreiecke in einem großen Dreieck bzw. um -30 Grad gedreht
.png)
.svg)
Für Tetraeder, Oktaeder und Ikosaeder haben wir folgende Oberflächennetze, wo die Fläche eines großes Dreieck so groß wie die Fläche von vier kleinen Dreiecken ist. Zur besseren Orientierung sind Kanten, die aneinander stoßen gleichfarbig skizziert, wobei je eine durchgängige Kante zu einer gleichfarbigen gestrichelten Kante gehört.
 Tetraeder.png)
Tetraeder
 Tetraeder.svg)
 Oktaeder.png)
Oktaeder
 Oktaeder.svg)
 Ikosaeder.png)
Ikosaeder
 Ikosaeder.svg)
Dann haben wir statt die kleinen Dreiecke grau zu färben, alle, die an einer Ecke eines großen Dreiecks liegen mit jeweils gleicher Farbe skizziert.
 Tetraeder bunt.png)
Tetraeder
 Tetraeder bunt.svg)
 Oktaeder bunt.png)
Oktaeder
 Oktaeder bunt.svg)
 Ikosaeder bunt.png)
Ikosaeder
 Ikosaeder bunt.svg)
Abstumpfen kleiner gleichfarbiger zusammenhängender Dreiecke ergibt
Tetraeder
Hexaeder
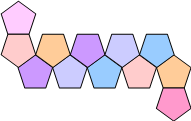
Dodekaeder
